Eikの微分音にLogic Pro X内蔵音源のSculptureを活用 [楽理]
私のブログでSculptureについて語るのは何年振りでしょうか。おそらく、坂本龍一の「きみについて」を語った時以来の事となると思いますが、微分音のSEを再現する為にSculpture活用はどれほど効果があるのか!? という事を語ってみようかと思います。
Sculptureの物理モデリングは非常に優秀なのでこうした企画を思い付くのでありますが、例えば金属音というのは材質や形状によっては必ずしも整数次の振動比で共鳴しようとはしない物です。通常、平易な自然数(=概ね低次の整数倍)での振動比という状況に於て器楽的な楽音は形成されておりますが、金属の場合はその形状や材質に依っては必ずしもオクターヴ回帰での安定的な振動比となる物ではありません。
実際にビブラフォンとて、目指す音高はオクターヴ回帰する音が際立って鳴る様にして作られておりますが、スペクトラム分析をするとオクターヴ回帰をしない螺旋律の部分音を含んでおり、オクターヴとは全く異なる、そうした整数倍の平易な振動比とは全く埒外となる周期で共鳴しようとする音を含んでいたりする物です。
除夜の鐘とて、あの振動比は鐘の構造から見れば安定的な共鳴ではあるのですが、器楽的な上方倍音列の自然数での共鳴とは全く異なる協和の姿である訳です。
昨年、小方厚が改訂した『音律と音階の科学』の中で「ポリゴノーラ」を紹介していた物でしたが、このポリゴノーラこそがまさに自然数で協和する体系のそれとは全く異なる螺旋律でオクターヴ回帰をしない音が「協和」状態となっているという事を示す例となる物であり、興味のある方は是非とも著書を手に取って読んでいただきたいと思います。
オクターヴ回帰をしない、あるいはオクターヴの近傍を取りつつも「絶対完全音程」という点で協和しようとしない状況は螺旋律とか呼ばれたりする物で、ウィリアム・セサレスはそうした体系の中のひとつとして、等間隔の微小音程が累積される音律構造を'Cents-Equal-Temperament'(=CET)として語っていたりします。
通常の、オクターヴ回帰を標榜する音律を「閉じた協和空間」と表現するとすれば、直線平均律法というのはオクターヴ回帰を目指していない「開いた」協和空間であると言えるでありましょう。直線平均律法については日本では田邉尚雄が詳らかにしていたと思いますが、Linear Temperament として呼ばれるそれを紹介していた事はあらためて驚きを禁じ得ない所です。
扨て、ガムランで代表される七平均律や五平均律というのは、実際には不揃いで、場合に依ってはオクターヴ回帰もしておらずオクターヴの近傍を採っている物もあるのですが、概ねオクターヴを標榜して5つとか7つを不揃い乍らも分割された音律があります。標榜する所が「等音程」でもあるので、不等分乍らも七等分平均律・五等分平均律としても決して誤りではありません。「等分平均律」として称さないのは各音程がいびつである不等分な音律となっているからでありますが、オクターヴを概ね5つと7つに分けるという事から整えられて等分となる5EDOや7EDOを機械的な指標で作られている音律も存在しますが、メタロフォンやゴング・チャイムで実際に用いられているそれらは不等分であり、オクターヴも拡張されたり狭まったりしているのが多岐に亙って存在しているのが実際です。
音律の観点から見て「スレンドロ」というのはオクターヴを「均等」に5つに分けた物として考える事ができます。他方「ペロッグ」は音組織としては7音であるものの、そこから5音が抜粋されて演奏されるという物であり且つオクターヴが拡張したり狭まったりするというのもペロッグの特徴であり、ガムランというのはスレンドロとペロッグの2つを併存させて用いるのだという事を念頭に置いていただければ、異なる2つの音律を用いている音楽という風にも理解に及ぶかと思います。
嘗てNHK-FMの『プログレ三昧』でも取り上げられたEikのアルバム『Hríslan og straumurinn』収録の同名タイトル曲「Hríslan og straumurinn」の冒頭のチャイムの音は、最初の音に対して2〜5番目のグループとなるチャイムとは音律が微妙に異なる物だという事がお判りになるかと思いますが、普段から微分音を取り扱う機会が少ない方からすれば、これらの「埒外」の音をどう判別しているのか全くピンと来ないかもしれませんが、耳が慣れて来ると判る様になるので是亦不思議な物です(笑)。

扨て下記に示すのは、スレンドロとペロッグが12等分平均律の基準からどの様に分布しているのかが理解できる音高対照図なのでありますが、これは
『ニュー・グローヴ世界音楽大事典』第2巻 p.90に掲載されているワシスト・スルヨディニングラット、スダルヨノ、スサント等のデータを援用した物であります。
こうした点を勘案すると、あらためてスレンドロとペロッグが併存しているが故にEikのそれも異なる音律が併存しているチャイムでフレージングされているという事がお判りになるかと思います。
EikのSEで用いられている音組織は、次の様な7EDOおよび5EDOとして表す事もできます。
7EDOの方はサジタルで表記しております。表記の使い分けなど「さしたる」問題でもないのでありますが、5EDOの方はKh accidentalフォントを用いて表しました。Khフォントを用いたのは、このフォントが四・六・八・十・十二・十六・二十・二十四分音(=24・36・48・60・72・96・120・144EDO)全てを表す事の出来る微分音変化記号が用意されているからであります。高次な自然数での整数倍となる純正音程を取り扱う場合は確かにサジタル表記も良いのですが、いかんせん覚えにくいという事もあり(苦笑)、多くの変化記号を用意していても視覚的にも峻別しやすいのはKhフォントであろうと思ったので用いる事にしました。
こうした音にあらためて注目してもらいたいのがもう一点、こうしたメタロフォンやゴング・チャイムが有している倍音としての部分音は、決して自然数の整数次倍音列としての振動比で構成されていないという点をあらためて知る必要があろうかと思います。
通常の器楽的な倍音構成ならば、非整数次の倍音成分を僅かに含んだとしても上方倍音列には2倍の振動比や3・4・5……倍という低次の協和的な振動比が顕著に現れる筈なのですが、先のガムランでのメタロフォンやゴング・チャイムではそうした倍音構成音となる部分音が現れないのが不思議な側面でもあります。2倍の音程比が現れるかと思いきや長七度よりも僅かに微小音程で高い所謂「クォーター・トーナル7th」が現れたりする物で、耳や脳には良い刺激となって届く物でもあります。
そうした螺旋律を大いに意識してもらう為にも、今回はApple Logic Pro X内蔵の物理モデリング音源であるSculptureを使ってEikの「Hríslan og straumurinn」のSE音を再現してみるとどうなるか!? という事を試す事にしました。Sculptureで用いる音はプリセットのグロッケンシュピールの音で、プリセットはディレイ音が噛ませてあるのでそれをカットしつつセント数を細かく設定すれば良いという、実に単純な設定で興味深い効果が得られるのであります。
なんやかんやで譜例動画を制作したのでありますが、本SEのフレーズ各音につき5つの部分音を抜粋して構成すれば、ある程度原曲のそれを再現可能であると判断したので、使用したのは25基のSculptureにて、譜例に示した通りに幹音からのセント数として音符に付与してある数字を入力すれば、概ね原曲に近い感じとして微分音の卒倒感を実感する事が可能になろうかと思います。
尚、Sculptureは物理モデリング音源の為、実際の楽器よりも音域を超えて発音する事が出来る事に依り、実際のグロッケンシュピールの発音可能音域を超えた記譜となっているのはご容赦下さい。最も高い音として記譜されているF♯9より僅かに高い近傍となる音は、特殊なグロッケンシュピールよりも1オクターヴ高くなってしまいますが、あくまでもこの譜例は部分音を抽出して器楽音を実現する為の物なので、実存する楽器のそれと乖離してしまっているという事を論う事はご勘弁願いたい所であります。
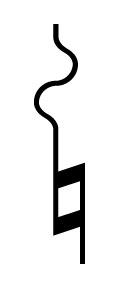
※譜例動画内 'Sculpture2' のパートの冒頭小節の3拍目の二分音符の箇所での変化記号ですが、付与されているセント数の表示は合っている物の充てるべき変化記号は下記の記号が正しい表記ですので茲に訂正します。
まあ、C9〜B9の音域が器楽音の組成に於て重要な音域かどうかの議論は扨措くとしても、その音域は「こもる or こもらない」音としてはいくら齢を重ねても認識可能となる音域であろうとは思うので、スペアナ片手に濾波せずに採譜したという訳です。
譜例動画の 'Sculpture 1' のパートの冒頭の音こそが、基本音となる [c] から数えて展開位置に還元した時には長七度よりも高くなる「クォーター・トーナル7th」に近しい音として表しています。この音はロ音からの派生音とするならば、付与されるセント数の数字は「+52」とするべきであろうかと思いますが、茲ではオクターヴ上の [c] から48セント低い「-48」としているのがご注意下さい。
Sculpture1とSculpture5とでの展開位置に還元した時の音程は「1152−39=1113セント」という事になる為、四分音体系でも使われるBセミ・シャープ=1150セントの音への音程差よりも長七度=1100セントの方が近いので、「クォーター・トーナル7th」と呼ぶ必要は無いのでは!? と疑問を抱かれる方も居られるかとは思います。
しかし四分音(=24EDO)体系で道う処のクォーター・トーナル7thとは、長七度と完全八度との間にある音であろうとも、長七度を超えた音程という所が重要であると私は考えるので、1150セントは他にもセミ・オクターヴとしても呼ばれますが、長七度を超える音程の「七度」を明示したかったのでこの様に記譜しているのです。
微分音を積極的に曲作りに活用する事は難しい事かもしれませんが、器楽音のアクセントとして微分音を音響的に活用する事は然程難しい事ではないと思います。そういう意味で、微分音をシンセなどの音作りに活用するTips的な意味で好意的に解釈していただければ之幸いであります。原曲の方も例示しておかなくてはいけませんね。下記動画の冒頭を参照ください。
Sculptureの物理モデリングは非常に優秀なのでこうした企画を思い付くのでありますが、例えば金属音というのは材質や形状によっては必ずしも整数次の振動比で共鳴しようとはしない物です。通常、平易な自然数(=概ね低次の整数倍)での振動比という状況に於て器楽的な楽音は形成されておりますが、金属の場合はその形状や材質に依っては必ずしもオクターヴ回帰での安定的な振動比となる物ではありません。
実際にビブラフォンとて、目指す音高はオクターヴ回帰する音が際立って鳴る様にして作られておりますが、スペクトラム分析をするとオクターヴ回帰をしない螺旋律の部分音を含んでおり、オクターヴとは全く異なる、そうした整数倍の平易な振動比とは全く埒外となる周期で共鳴しようとする音を含んでいたりする物です。
除夜の鐘とて、あの振動比は鐘の構造から見れば安定的な共鳴ではあるのですが、器楽的な上方倍音列の自然数での共鳴とは全く異なる協和の姿である訳です。
昨年、小方厚が改訂した『音律と音階の科学』の中で「ポリゴノーラ」を紹介していた物でしたが、このポリゴノーラこそがまさに自然数で協和する体系のそれとは全く異なる螺旋律でオクターヴ回帰をしない音が「協和」状態となっているという事を示す例となる物であり、興味のある方は是非とも著書を手に取って読んでいただきたいと思います。
オクターヴ回帰をしない、あるいはオクターヴの近傍を取りつつも「絶対完全音程」という点で協和しようとしない状況は螺旋律とか呼ばれたりする物で、ウィリアム・セサレスはそうした体系の中のひとつとして、等間隔の微小音程が累積される音律構造を'Cents-Equal-Temperament'(=CET)として語っていたりします。
通常の、オクターヴ回帰を標榜する音律を「閉じた協和空間」と表現するとすれば、直線平均律法というのはオクターヴ回帰を目指していない「開いた」協和空間であると言えるでありましょう。直線平均律法については日本では田邉尚雄が詳らかにしていたと思いますが、Linear Temperament として呼ばれるそれを紹介していた事はあらためて驚きを禁じ得ない所です。
扨て、ガムランで代表される七平均律や五平均律というのは、実際には不揃いで、場合に依ってはオクターヴ回帰もしておらずオクターヴの近傍を採っている物もあるのですが、概ねオクターヴを標榜して5つとか7つを不揃い乍らも分割された音律があります。標榜する所が「等音程」でもあるので、不等分乍らも七等分平均律・五等分平均律としても決して誤りではありません。「等分平均律」として称さないのは各音程がいびつである不等分な音律となっているからでありますが、オクターヴを概ね5つと7つに分けるという事から整えられて等分となる5EDOや7EDOを機械的な指標で作られている音律も存在しますが、メタロフォンやゴング・チャイムで実際に用いられているそれらは不等分であり、オクターヴも拡張されたり狭まったりしているのが多岐に亙って存在しているのが実際です。
音律の観点から見て「スレンドロ」というのはオクターヴを「均等」に5つに分けた物として考える事ができます。他方「ペロッグ」は音組織としては7音であるものの、そこから5音が抜粋されて演奏されるという物であり且つオクターヴが拡張したり狭まったりするというのもペロッグの特徴であり、ガムランというのはスレンドロとペロッグの2つを併存させて用いるのだという事を念頭に置いていただければ、異なる2つの音律を用いている音楽という風にも理解に及ぶかと思います。
嘗てNHK-FMの『プログレ三昧』でも取り上げられたEikのアルバム『Hríslan og straumurinn』収録の同名タイトル曲「Hríslan og straumurinn」の冒頭のチャイムの音は、最初の音に対して2〜5番目のグループとなるチャイムとは音律が微妙に異なる物だという事がお判りになるかと思いますが、普段から微分音を取り扱う機会が少ない方からすれば、これらの「埒外」の音をどう判別しているのか全くピンと来ないかもしれませんが、耳が慣れて来ると判る様になるので是亦不思議な物です(笑)。

扨て下記に示すのは、スレンドロとペロッグが12等分平均律の基準からどの様に分布しているのかが理解できる音高対照図なのでありますが、これは
『ニュー・グローヴ世界音楽大事典』第2巻 p.90に掲載されているワシスト・スルヨディニングラット、スダルヨノ、スサント等のデータを援用した物であります。
こうした点を勘案すると、あらためてスレンドロとペロッグが併存しているが故にEikのそれも異なる音律が併存しているチャイムでフレージングされているという事がお判りになるかと思います。
EikのSEで用いられている音組織は、次の様な7EDOおよび5EDOとして表す事もできます。
7EDOの方はサジタルで表記しております。表記の使い分けなど「さしたる」問題でもないのでありますが、5EDOの方はKh accidentalフォントを用いて表しました。Khフォントを用いたのは、このフォントが四・六・八・十・十二・十六・二十・二十四分音(=24・36・48・60・72・96・120・144EDO)全てを表す事の出来る微分音変化記号が用意されているからであります。高次な自然数での整数倍となる純正音程を取り扱う場合は確かにサジタル表記も良いのですが、いかんせん覚えにくいという事もあり(苦笑)、多くの変化記号を用意していても視覚的にも峻別しやすいのはKhフォントであろうと思ったので用いる事にしました。
こうした音にあらためて注目してもらいたいのがもう一点、こうしたメタロフォンやゴング・チャイムが有している倍音としての部分音は、決して自然数の整数次倍音列としての振動比で構成されていないという点をあらためて知る必要があろうかと思います。
通常の器楽的な倍音構成ならば、非整数次の倍音成分を僅かに含んだとしても上方倍音列には2倍の振動比や3・4・5……倍という低次の協和的な振動比が顕著に現れる筈なのですが、先のガムランでのメタロフォンやゴング・チャイムではそうした倍音構成音となる部分音が現れないのが不思議な側面でもあります。2倍の音程比が現れるかと思いきや長七度よりも僅かに微小音程で高い所謂「クォーター・トーナル7th」が現れたりする物で、耳や脳には良い刺激となって届く物でもあります。
そうした螺旋律を大いに意識してもらう為にも、今回はApple Logic Pro X内蔵の物理モデリング音源であるSculptureを使ってEikの「Hríslan og straumurinn」のSE音を再現してみるとどうなるか!? という事を試す事にしました。Sculptureで用いる音はプリセットのグロッケンシュピールの音で、プリセットはディレイ音が噛ませてあるのでそれをカットしつつセント数を細かく設定すれば良いという、実に単純な設定で興味深い効果が得られるのであります。
なんやかんやで譜例動画を制作したのでありますが、本SEのフレーズ各音につき5つの部分音を抜粋して構成すれば、ある程度原曲のそれを再現可能であると判断したので、使用したのは25基のSculptureにて、譜例に示した通りに幹音からのセント数として音符に付与してある数字を入力すれば、概ね原曲に近い感じとして微分音の卒倒感を実感する事が可能になろうかと思います。
尚、Sculptureは物理モデリング音源の為、実際の楽器よりも音域を超えて発音する事が出来る事に依り、実際のグロッケンシュピールの発音可能音域を超えた記譜となっているのはご容赦下さい。最も高い音として記譜されているF♯9より僅かに高い近傍となる音は、特殊なグロッケンシュピールよりも1オクターヴ高くなってしまいますが、あくまでもこの譜例は部分音を抽出して器楽音を実現する為の物なので、実存する楽器のそれと乖離してしまっているという事を論う事はご勘弁願いたい所であります。
※譜例動画内 'Sculpture2' のパートの冒頭小節の3拍目の二分音符の箇所での変化記号ですが、付与されているセント数の表示は合っている物の充てるべき変化記号は下記の記号が正しい表記ですので茲に訂正します。

まあ、C9〜B9の音域が器楽音の組成に於て重要な音域かどうかの議論は扨措くとしても、その音域は「こもる or こもらない」音としてはいくら齢を重ねても認識可能となる音域であろうとは思うので、スペアナ片手に濾波せずに採譜したという訳です。
譜例動画の 'Sculpture 1' のパートの冒頭の音こそが、基本音となる [c] から数えて展開位置に還元した時には長七度よりも高くなる「クォーター・トーナル7th」に近しい音として表しています。この音はロ音からの派生音とするならば、付与されるセント数の数字は「+52」とするべきであろうかと思いますが、茲ではオクターヴ上の [c] から48セント低い「-48」としているのがご注意下さい。
Sculpture1とSculpture5とでの展開位置に還元した時の音程は「1152−39=1113セント」という事になる為、四分音体系でも使われるBセミ・シャープ=1150セントの音への音程差よりも長七度=1100セントの方が近いので、「クォーター・トーナル7th」と呼ぶ必要は無いのでは!? と疑問を抱かれる方も居られるかとは思います。
しかし四分音(=24EDO)体系で道う処のクォーター・トーナル7thとは、長七度と完全八度との間にある音であろうとも、長七度を超えた音程という所が重要であると私は考えるので、1150セントは他にもセミ・オクターヴとしても呼ばれますが、長七度を超える音程の「七度」を明示したかったのでこの様に記譜しているのです。
微分音を積極的に曲作りに活用する事は難しい事かもしれませんが、器楽音のアクセントとして微分音を音響的に活用する事は然程難しい事ではないと思います。そういう意味で、微分音をシンセなどの音作りに活用するTips的な意味で好意的に解釈していただければ之幸いであります。原曲の方も例示しておかなくてはいけませんね。下記動画の冒頭を参照ください。
2019-09-09 11:00